Godot: Dive into Shaders

Shader im Kontext von Grafikprogrammierung haben mich schon immer fasziniert. Sie kommen sowohl bei Videospielen in den Einsatz, als auch in Filmen. Mit der weiteren Digitalisierung, dem Aufstieg von XR wird diese Technologie immer wichtiger. Wirklich verstanden habe ich sie noch nicht. Eigene Shader schreiben schon gar nicht.

Für diesen Beitrag habe ich mir vorgenommen, mich diesem Umstand anzunehmen und mehr über Shader zu lernen. Als Entwicklungsumgebung fiel die Wahl auf die Open-Source-Engine Godot.

Was sind Shader?

Shader ist ein Sammelbegriff für Programme, welche auf der Grafikkarte ausgeführt werden. In unserem Kontext sprechen wir davon, dass wir Shader verwenden, um Aussehen, Form und Farbe von Objekten im 2D- oder 3D-Raum zu verändern. Sie können Gras im Wind wehen lassen, einen Ozean zu leben erwecken oder Fußabdrücke im Schnee simulieren.

Warum also Shader verwenden? Sie sind schnell – sehr schnell. Grafikkarten sind darauf optimiert, viele Berechnungen parallel durchzuführen. Warum bspw. die Pixel eines Bilds nacheinander berechnen, wenn sie doch unabhängig voneinander sind?

Diese Umstand, dass bspw. die Farbe mehrere Pixel parallel, zeitgleich berechnet wird, begründet, warum viele Entwickler:innen zunächst Probleme mit dem Schreiben von Shadern haben.

Was macht Shader besonders?

Shading-Sprachen wie die bekannte OpenGL Shading Language (GLSL) definieren klar, wie Shader geschrieben werden und das unterscheidet sich ein wenig von dem Ansatz wie anderweitig Software entwickelt wird.

Würden wir beispielsweise eine gesamte Textur in einer beliebigen Farbe färben wollen, wäre ein bekannter Ansatz:

for x in range(width):
  for y in range(height):
    set_color(x, y, some_color)

Doch im Kontext von Shadern, soll ja schließlich der Code für jeden Pixel parallel ausführbar sein. Wir befinden uns sozusagen schon in einem Loop. Richtig wäre:

void fragment() {
  COLOR = some_color;
}

Die Grafikkarte ruft für jeden Pixel die fragment() Funktion auf, gibt eine Vielzahl an Variablen preis, darunter COLOR, um die Farbe des aktuellen Pixels zu bestimmen.

Von diesen Funktionen gibt es mehrere, von den Variablen noch viel mehr. Die fragment() Funktion wird für jeden Pixel aufgerufen. vertex() für jede Vertex in einem Mesh, light() für jeden Pixel und jede Lichtquelle. Diese Liste ist leicht unterschiedlich je nachdem welche Shading-Language man verwendet und in welcher Entwicklungsumgebung.

Im Falle von Godot gibt es noch ein wenige weitere Funktionen, welche zunächst nicht wichtig sind. Ich beschränke mich zunächst auf fragment() und vertex().

Ein erster Versuch

Für den ersten Shader verwenden wir eine schlichte, zweidimensionale Textur, hier das Logo der Godot Game Engine. Wenden wir hier nun das Beispiel aus dem vorherigen Teil an. Wir wollen die Textur vollständig in einer beliebigen Farbe einfärben.

void fragment(){
  COLOR = vec4(0.4, 0.6, 0.9, 1.0);
}

Dieser Shader färbt unsere Textur in ein sanftes Blau. Die Built-In Variable COLOR wird mit einem vec4 überschrieben, welcher die rgba-Werte (zwischen 0.0 und 1.0 für die dem entsprechende Farbe enthält. Bedeutet, dass jedem Pixel diese Farbe zugewiesen wird.

Wie würde man nun einen Farbverlauf realisieren. Für einen Farbverlauf bräuchten wir die Information, für welchen Pixel auf der Textur die fragment() Funktion ausgeführt wird. Schließlich bleibt der Code für jeden Pixel der selbe.

Für diesen Zweck ist UV Variable. Die sogenannten UV-Koordinaten werden von einem vec2 gebildet, welcher mit Werten zwischen 0.0 und 1.0 eine Aussage trifft, auf welcher Position wir uns befinden. Dabei ist 0.0 links oben und 1.1 rechts unten, auf der Textur.

Glücklicherweise ist GLSL sehr tolerant was Datentypen angeht. Wir können also einen vec4 auch mittels zwei vec2 initialisieren, oder eine Mischung davon. Der Compiler übernimmt den Rest.

void fragment() {
  COLOR = vec4(UV, 0.5, 1.0);
}

Dieser Shader sorgt demnach dafür, dass je nach UV-Koordinate die Werte für den roten und den grünen Farbkanal des vec4 verändert werden. Je weiter rechts der Pixel liegt, desto weiter näher sich u dem Wert 1.0 an und damit einem grellen Rot. Das gleiche gilt für v. Unten Links, wo UV == vec2(1,1), werden die Pixel gelb eingefärbt.

Bewegung

Wir wenden uns heute der vertext() Funktion unseres Shaders zu. Zur Wiederholung: Diese Funktion wird für jeden Vertex eines Mesh ausgeführt. Da wir aktuell uns nur mit einer 2D-Textur auseinandersetzen, sind das die vier Eckpunkte der Textur, bedeutet die Funktion wird für jede der vier Vertices aufgerufen.

void vertex() {
  VERTEX += vec2(10.0, 0.0);
}

Dieser Vertex-Shader würde also jeden Vertex um 10 Einheiten auf der x-Achse verschieben. Folglich würde unsere Textur weiter rechts gerendert werden. Wichtig: Die Position der Textur, bspw. für die Berechnung von Kollisionen o.Ä. verändert sich nicht.

Um das gesamte Beispiel etwas dynamischer zu machen, werden wir unsere Textur dazu bringen, sich im Kreis zu bewegen. Bewegung benötigt Zeit, worauf wir mit der built-in Variable TIME Zugriff haben. Grob erklärt: TIME beschreibt die Zeit in Sekunden seit dem Start der Anwendung. Diese Variable können wir als Parameter für Sinus- und Cosinus-Funktionen werden, auch Funktionen, welche uns zur Verfügung stehen.

void vertex() {
  VERTEX += vec2(cos(TIME) * 100.0, sin(TIME) * 100.0);
}

sin() und cos() geben uns Werte zwischen 0.0 und 1.0 zurück. Was herzlich schlecht zu sehen ist. Darum multiplizieren wir die Werte mit einem konstanten Wert, um die Bewegung sichtbarer zu machen – der Radius, wenn man so möchte.

Runden wir das Ganze ab, indem wir von außerhalb des Shaders bestimmen können, wie groß dieser Radius sein soll.

uniform float radius = 100.0;

void vertex() {
    VERTEX += vec2(cos(TIME) * radius, sin(TIME) * radius);
}

Wir definieren eine uniform Variabel, welche wir über unsere Code-Basis verändern können, oder im Falle von Godot zusätzlich über die GUI.

Wir können also nun auch Vertices unserer Textur verändern! Doch zwei Dimensionen sind auf Dauer etwas langweilig.

Die dritte Dimension

Unser Ziel ist es, eine Fläche in die dritte Dimension zu verkrümmen. Dazu verwenden wir natürlich die vertex() Funktion. Problem ist, dass unsere bisherige Fläche nur von vier Vertices definiert wurde.

Wenig Freiheit für ausgefallene Formen. Also verwenden wir für unser Experiment eine Fläche mit 32 Subdivisions. Damit stehen uns knapp 1.500 Vertices zur Verfügung.

void vertex() {
    VERTEX.y += cos(VERTEX.x);
}

In diesem Fall verändern wir für jeden Vertex die y-Koordinate. Verschieben ihn also nach oben oder unten. In Verwendung kommt wieder die cos() Funktion, welche uns Werte zwischen 0.0 und 1.0 in einem wellenförmigen Verlauf bietet.

Als Parameter nehmen wir die x-Koordinate desselben Vertex. Die Fläche krümmt sie also auf der x-Achse, mit einem Höhepunkt auf der (0,0) Koordinate. Eine vollständige Welle sehen wir aber nicht.

Das liegt daran, dass die momentanen x-Werte unserer Verticies zwischen -1.0 und 1.0 liegen. Unsere quadratische Fläche liegt am Ursprung (0,0) mit einer Seitenlänge von 1.0. Multiplizieren wir eine konstante dazu, lässt sich der wellenförmige Charakter der Cosinus-Funktion sichtbar machen.

void vertex() {
    VERTEX.y += cos(VERTEX.x * 4.0);
}

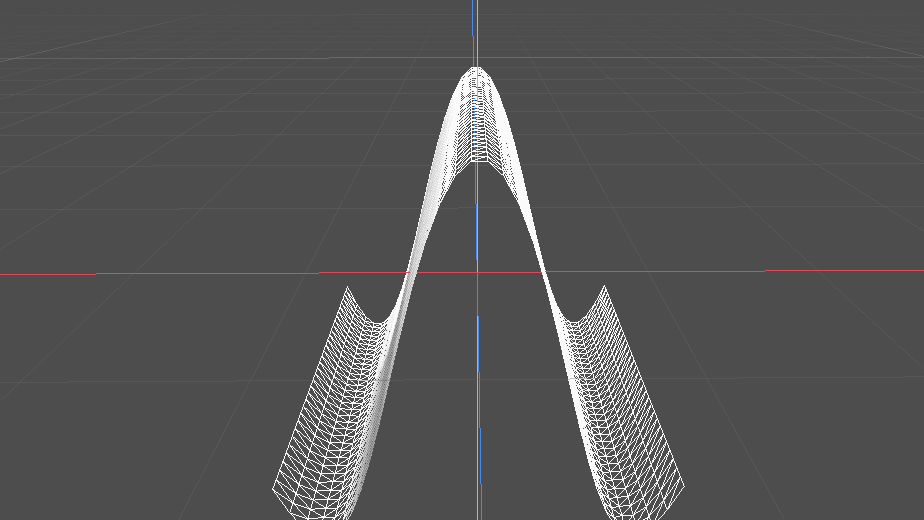
Das selbe funktioniert auch indem wir die z-Achse als Parameter nehmen. Diesmal krümmt sich die Fläche dann über die z-Achse. Spannend wird es, wenn wir beide Werte miteinander multiplizieren.

void vertex() {
    VERTEX.y += cos(VERTEX.x * 4.0) * cos(VERTEX.z * 4.0);
}

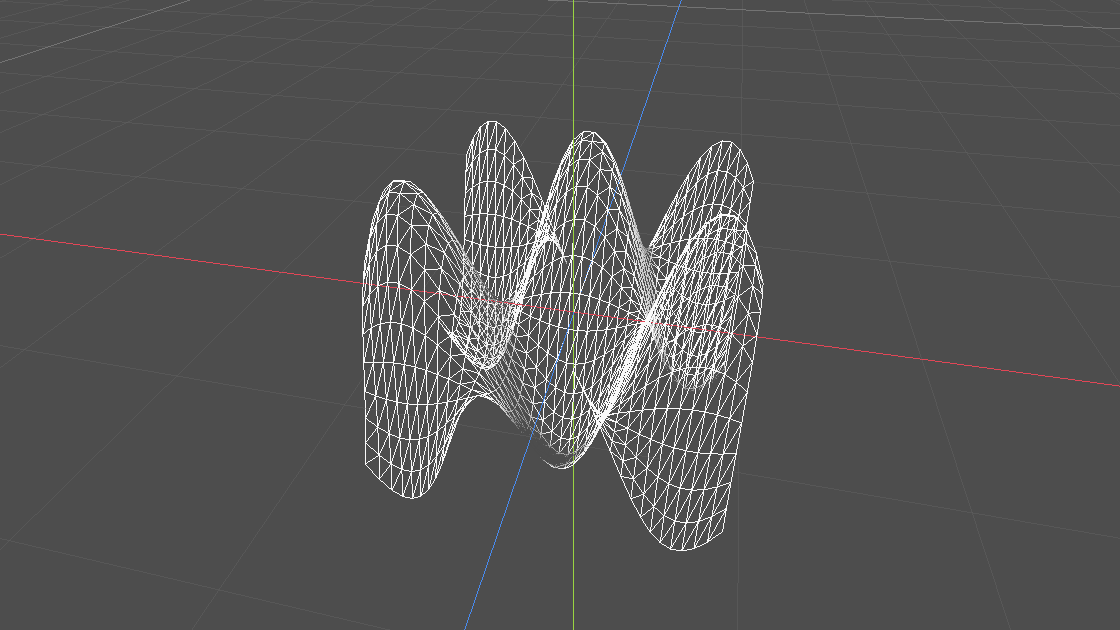
In diesem Fall erreichen wir damit eine sehr regelmäßige Hügellandschaft. Genauer gesagt fünf Hügel. Ergebnisse beider cos() Funktionen werden sozusagen miteinander vermischt. Die beiden Verkrümmungen der x-Achse und der y-Achse werden vereint.

Soweit so gut! Wir haben aus einer langweiligen Fläche eine dreidimensionale Form erschaffen und das nur mithilfe von wenigen Zeilen Code.

Das Chaos nutzen

An diesem Punkt dämmert es vielleicht der ein oder anderen Person schon. Mithilfe einer Zeile Code, konnten wir eine relativ komplexe Form erschaffen und diese mit wenigen Parametern verändern. Ausgeführt auf der Grafikkarte – in Sekundenschnelle. Da ist viel Potenzial drin.

Wir können also unsere Vertices mithilfe des Shaders in der Höhe verschieben. Um das ganze etwas aufregender zu gestalten, brauchen wir Werte, am besten zwischen 0.0 und 1.0, welche möglichst zufällig, aber homogen verteilt sind. Die Antwort auf diese Suche lauter: Noise-Texture.

Eine NoiseTexture liefert uns für jeden Pixel einen Helligkeitswert zwischen 0.0 und 1.0, welchen wir als Parameter für unsere Höheninformation der Vertices verwenden können.

uniform sampler2D noise;

void vertex() {
    float height = texture(noise, VERTEX.xz).r;
    VERTEX.y += height;
}

In Godot lässt sich solch eine Noise-Texture leicht generieren. Mithilfe eines uniform können wir sie als Parameter im Shader definieren. Anschließend verwenden wir texture(), um über den x und z Wert des Vertex den Wert des roten Farbkanals der Textur zu erhalten. Warum Rot? Noise-Texturen sind in der Regel schwarz-weiß. Alle Farbkanäle haben somit den selben Wert. Wir könnten also auch den grünen oder blauen Farbkanal verwenden.

Nun sehen unsere Berge noch etwas sehr spitz und unförmig aus. Runden wir diese ab, indem wir einen Skalar bestimmen, welcher die hohen Werte etwas reduziert.

uniform sampler2D noise;
uniform float height_scale = 0.5;

void vertex() {
    float height = texture(noise, VERTEX.xz).x;
    VERTEX.y += height * height_scale;
}

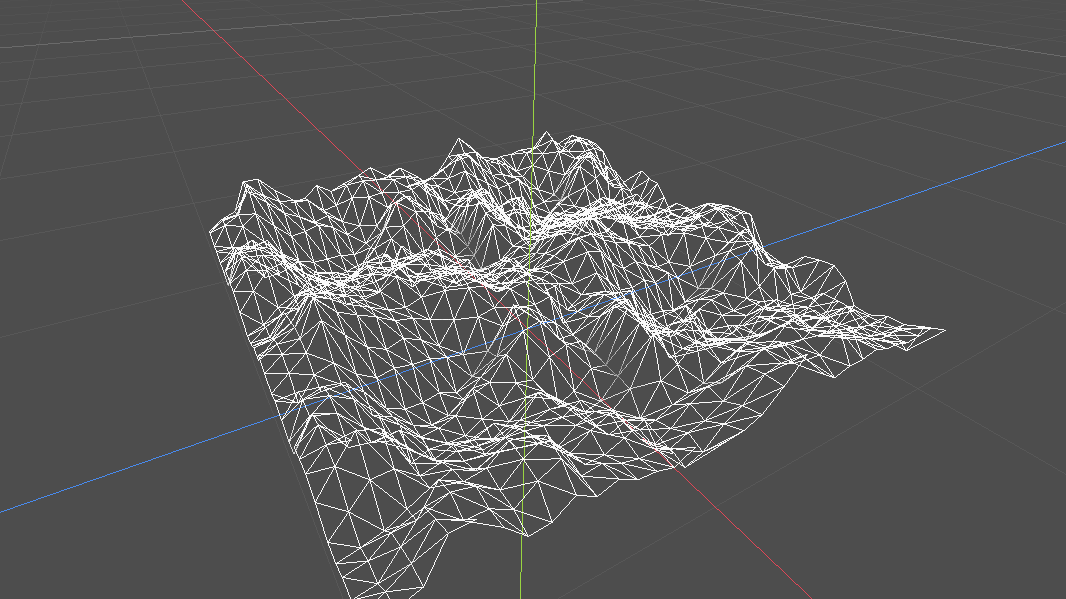
Damit sehen die Berge schon etwas realistischer aus. Mit nur wenigen Schritten, wird aus unserer Fläche eine realistische Berglandschaft, welche wir mit wenigen Reglern beeinflussen können. Beeindruckend!

Berge bewegen

Die Wireframe-Ansicht war bisher nur dafür nützlich, besser nachzuvollziehen, wo Vertices liegen. Wenn wir diese nun wieder deaktivieren, sehen wir unsere Berglandschaft keinerlei Schatten wirft. Das liegt daran, dass wir zwar das Mesh verformt, aber die NORMALS, welche für die Schattenberechnung notwenig sind, nicht aktualisiert haben.

Würden wir momentan ein Licht inmitten der Landschaft setzen, würde keine korrekte Schattenberechnung stattfinden.

Normals kann man sich vorstellen wie Normalvektoren einzelner Flächen eines Meshs. Diese Vektoren werden unter anderem verwendet, um zu bestimmen, wie hell die Fläche gerendert werden soll. Des weiteren gibt es eine Technik, genannt Normal-Map, welche diese Vektoren mithilfe von Farbwerten in einer zweidimensionalen Textur codiert.

In Godot ist es relativ einfach möglich eine beliebige Noise-Textur als eine solche Normal-Map zu verwenden. Wir werden diese Normal-Map allerdings in fragment() verwenden und für jeden Pixel anwenden und nicht nur für jeden Vertex.

Nun stellt sich die Frage, wie wir dafür sorgen, dass sowohl vertex(), als auch fragment() die selbe Position verwenden, um von ihrer jeweiligen Textur zu lesen. Mittels dem varying Keyword lassen sich Variablen über Funktionen hinweg speichern.

uniform float height_scale = 0.5;
uniform sampler2D noise;
uniform sampler2D normalmap;

varying vec2 tex_position;

void vertex() {
  tex_position = VERTEX.xz / 2.0 + 0.5;
  float height = texture(noise, tex_position).x;
  VERTEX.y += height * height_scale;
}

void fragment() {
  NORMAL_MAP = texture(normalmap, tex_position).xyz;
}

Damit haben wir mit wenigen Schritten eine Berglandschaft erschaffen, welche korrekt auf Licht reagiert. Die Werte lassen sich beliebig anpassen. Es wäre möglich die Fläche größer zu skalieren und so eine größere Landschaft abzudecken und ggf. einen Hintergrund damit auszukleiden.

Fazit

Nach diesem kleinen Exkurs, habe ich meine initiale Zurückhaltung gegenüber dem Thema Shader überwunden. Das Ganze hat mir gezeigt, wie mächtig Shader sind, aber auch, dass es unkonventionelles Denken benötigt, um bestimmte Effekte zu erzielen.

In Zukunft hoffe ich mehr in dem Bereich lernen zu können. Für jetzt werde ich zweimal nachdenken, ob ich bei einem grafischen Herausforderung nicht mit einem Shader lösen kann.